Entropy is one of the key concepts of information theory, data science and machine learning. Understanding the math behind it is crucial for designing solid machine learning pipelines. Therefore, in this post, I try to explain the entropy as simple as possible.
When I first saw the name entropy in decision trees, I really didn’t think about it. I couldn’t get the importance of this concept. So, I moved on to my machine learning (ML) adventure without it. However, almost every time I tried to learn a new ML concept, entropy was on my way. I couldn’t escape from it. Then, I (with the encouragement of my graduate advisor who is an excellent mentor for me) decided to confront it. The first few days to understand the entropy was not easy in terms of understanding why it was created in the first place. We already have the probability, haven’t we? But, no. It is very useful, fix some problems that the probability can’t, and almost every concept in ML make use of it due to some computational reasons.
In this first story of mine, I will try my best to clear out the concepts of entropy and some other related concepts such as information gain and information gain ratio. I also want to suggest a video about entropy by Luis Serrano. You can find the video here. While this is an excellent video, it is not enough to fully understand the entropy. You need to make lots of reading sessions and maybe implement it with a programming language. Now, let’s get back to the subject.
I am not a physicist but as far as I know, entropy in physics corresponds to the energy of particles in a media. If we give an example, the four phases of matter would be a good candidate.
This idea applies to the information theory in the sense of probability. Claude Shannon is the man who brings the idea in information theory. Suppose you have a computer. This computer can only output a sequence of characters. But some characters are permitted to repeat. The list of all possible characters that can present in the output is the dictionary of the computer. The question is here how much information do you have about the output of the computer?

The above computer has a dictionary \(D = \{ \text{"A"} \}\). So, we will have a guaranteed output of “A”, right? This means that we know a lot about the output. We will get into how we will compute entropy, but at this point let’s say that this output has an entropy value of 0. Because we are certain about the output. It will consist of nothing else but the letter “A” only.
What if our dictionary consists of more than one letter or even numbers? For example, dictionary \(D = \{ \text{"A"}, \text{"B"} \}\). Then the output of the computer might be as follows.

Let’s say from this output we need to pick a letter. Remember that each pick is independent of each other. So, what is the probability of producing an output that has the same order as in the original output sequence? The answer to this question is comes from the probability, right?
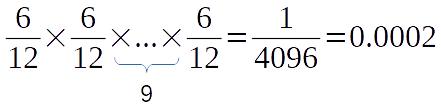
As you can see, the result is very small. This means that producing the same output as the computer is very difficult. We have little information about the output. Our chance to pick a letter and knowing what it is is the same as tossing a coin. This result suggests us we have a higher entropy value here.
But why do we need the entropy? We have the probability and it tells us something about the information amount of the data. Here is the reason. Actually, you can see it yourself, too. If we have fewer letters in the sequence, let’s say 4 instead of 12; two for “A” and two for “B”, the result will be 0.0625. But the entropy will still be high. So, what’s change? You see that the amount of letters in the data affects the output of the probability exponentially. This is a problem for our computers, right? Smaller the floating point number, smaller the precision. You may be heard of the vanishing gradient problem in Recurrent Neural Networks (RNN). This is the reason for it and this is the starting point of entropy.
We need a way to not reducing the output that much but at the same time take care of all the letters in the sequence. What if we try to get rid of the exponential function (the repeated multiplication) by converting it to a linear function. How do we do that? Maybe the answer is in the summation. Because repeated summation is just a linear function, unlike multiplication. So, the conversion can be easily made by logarithms. Then let’s take the logarithm of the above equation. There is only a little problem here. Which number should be used as the base of the logarithm? You can pick whatever number you want. However, we are from the area of computation. We love to express numbers and information as bits. A bit is a 1 or 0. So, a bit can be expressed in base 2. This means that we want to express the data with two symbols. Therefore, it is natural that we choose 2 as the base for the logarithm. Now, let’s take the logarithm at base 2.
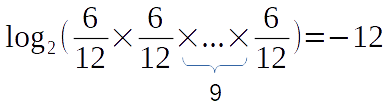
What a beautiful number here. But, hmm…, you see there are two little problems here. First, we have 12 letters in the sequence and the result is 12. Will this number increase as the letter count increases? Yes, it will increase. So we can normalize it with the letter count by dividing it to 12 in this case.
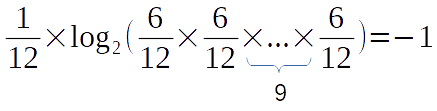
This is much better. But, why the number is negative? There is no point to proceed with a negative number while trying to measure the information in a sequence. So, let’s multiply the expression with -1.
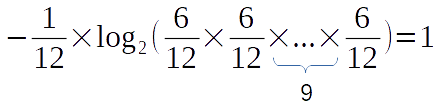
This is it. We made to the end. Almost. We still haven’t converted the multiplication into the summation.
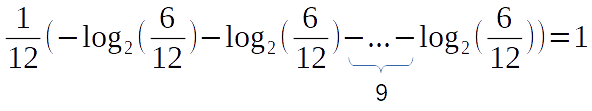
The first six expressions of the sequence are for the letter “A” and the remaining six is for the letter “B”. Now, let’s make this more obvious and distribute the multiplication over the whole expression.
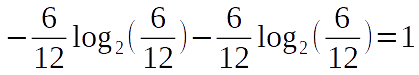
This is the entropy. For this sequence, as we change the number of letters, the probability of producing the exact same output will change. However, the entropy will never change as the proportion of letter counts are constant regardless of the total number of letters in the sequence. If we generalize the entropy, the following expression can be obtained.
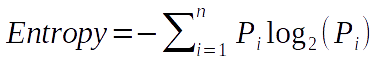
\(P\) is the probability of picking ith distinct element from the sequence. The knowledge and entropy are opposites. If we have high knowledge about a sequence, the entropy is lower, and vice versa. Let’s make another example with a different sequence.

Here we have 3 distinct letters in a 12 letter sequence. Let’s calculate the entropy with the above formula.
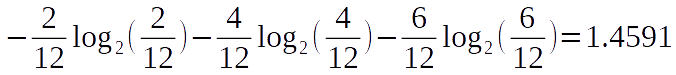
Ok, we have calculated the entropy. But, what’s the result even means? Actually, the result is the average number of yes/no questions to guess the next letter in the sequence. Be careful about that. You need to ask the questions in the smartest way possible.
Entropy is used in many ML methods. One of the popular ML methods is Decision Tree. In the decision tree, we try to find the independent variable that splits another dependent variable in the best way possible. How to find that variable? The answer is we split the target (dependent) variable with each of the other independent variables and check the reduction in entropy after each of the splits. The variable that causes the most reduction is the winner. This reduction is called information gain.
There are other types of entropy reduction metrics. For example, information gain ratio. It is a very close concept to information gain. I am planning to write about each of them later in separate stories. I hope this post is helpful. If I made a mistake in the post, please let me know. See you soon. Bye…


